The ability to efficiently move in a complex environment is a key property of animals. It is central to their survival, i.e. to avoid predators, to look for food, and to find mates for reproduction (Ijspeert, 2008). Nature has found different solutions for the problem of legged locomotion. For example, the vertebrate animals have a spinal column and one or two pairs of limbs that are used for walking. Arthropoda animals are characterized by a segmented body that is covered by a jointed external skeleton (exoskeleton), with paired jointed limbs on each segment and they can have a high number of limbs (Carbone & Ceccarelli,2005). The biological mechanisms underlaying locomotion have therefore been extensively studied by neurobiologists, and in recent years there has been an increase in the use of computer simulations for testing and investigating models of locomotor circuits based on neurobiological observations (Ijspeert, 2001). However, the mechanisms generating the complex motion patterns performed by animals are still not well understood (Manoonpong,2007).
Animal locomotion, for instance, requires multi-dimensional coordinated rhythmic patterns that need to be correctly tuned so as to satisfy multiple constraints: the capacity to generate forward motion, with low energy, without falling over, while adapting to possibly complex
terrain (uneven ground, obstacles), and while allowing the modulation of speed and direction (Ijspeert & Crespi, 2007). In vertebrate animals, an essential building block of the locomotion controller is the Central Pattern Generator (CPG) located in the spinal cord. The CPG is a
neural circuit capable of producing coordinated patterns of rhythmic activity in open loop, i.e. without any rhythmic inputs from sensory feedback or from higher control centers (Delcomyn, 1980; Grillner, 1985). Interestingly, very simple input signals are sufficient to
modulate the produced patterns. Furthermore, CPG can adapt to various environments by changing the periodic rhythmic patterns. For instance, the cats and horses are able to change their locomotor patterns depending on the situation.
This relevance of locomotion both for biology and for robotics has led to multiple interesting interactions between the two fields. The interactions have mainly been in one direction, with robotics taking inspiration from biology in terms of morphologies, modes of locomotion,
and/or control mechanisms. In particular, many robot structures are directly inspired by animal morphologies, from snake robots, quadruped robots, to humanoid robots.
Increasingly, robotics is now providing something back to biology, with robots being used
as scientific tools to test biological hypotheses (Ijspeert, 2008). Researchers have studied the CPGs for decades and some principles have been derived to model their functionality and structure. CPGs have been proposed as a mechanism to generate an efficient control strategy for legged robots based on biological locomotion principles. Locomotion in legged robots is much more complex than wheeled robots, since the formers have between twelve or twenty degrees of freedom, which must be rhythmically coordinated to produce specific gaits. The design of locomotion control systems of legged robots is a challenge that has been partially solved. To develop bio-inspired solutions, detailed analyses of candidate biological neural systems are essential as in the case of legged locomotion.
Models of CPGs have been used to control a variety of different types of robots and different modes of locomotion. For instance, CPG models have been used with hexapod and octopod robots inspired by insect locomotion, quadruped robots inspired by vertebrates, such as horse, biped robots inspired by humans and other kind of robots inspired by reptiles, such as snakes, as it will be discussed in the section 2. CPGs could been modeled with different levels of abstraction, these aspects will be presented in section 3. Additionally, CPGs present several interesting properties including distributed control, the ability to deal with redundancies, fast control loops, and allowing modulation of locomotion by simple control signals. These properties, when transferred to mathematical models, make CPGs interesting building blocks for locomotion controllers in robots (Fujii et al., 2002; Ijspeert, 2008), as shown in section 4.
In spite of its importance, the CPG-approach presents several disadvantages. One of the main drawbacks of CPGs is related with the learning methodologies to generate the rhythmic signals (Zielinska, 1996). For that purpose, a method to tune a CPG using genetic algorithms (GA) is proposed, whose details are provided in section 5. Moreover, a methodology for designing CPGs to solve a particular locomotor problem is yet missing. Other problem is that animals rarely perform steady-state locomotion for long time, and tend to superpose, and switch between, multiple motor behaviors. A remaining open challenge is therefore to design control architectures capable of exhibiting such richness motor skills.
Engineering CPG-based control systems has been difficult since the simulation of even rather simple neural network models requires a significant computational power that exceeds the capacity of general embedded microprocessors. As a result, CPG dedicated hardware implementations, both analog and digital, have received more attention (Nakada, 2003). On one hand, analog circuits have been already proposed, being computation and power efficient but they usually lack flexibility and dynamics and they involve large design cycles. On the other hand, Field-Programmable Gate Array (FPGA) substrate might provide real-time response, low power consumption and concurrent processing solutions for low-level locomotion issues (Barron-Zambrano et al., 2010b). So, a brief analysis of CPG implementations is presented in section 6. Also, the integration of environment information might allow to produce behaviors by means of selection and adaption of lower substrates. Under this scenario, legged robots may reconfigure their locomotion control strategies on-line according to sensory information so as to effectively handle dynamic changes in the real world. Yet, the FPGA-based approach fits well since it could handle efficiently higher perception functions for CPG parameter adaptation, and to provide the neural processing and coordination of a custom and adaptive CPG hardware module. For those reasons, section 7 presents a hardware implementation for quadruped locomotion control based on FPGA. The experimental results of hardware implementation and the future work are shown in sections
8 and 9, respectively. Finally, the conclusions of this work are presented in section 10.
Locomotion solution methods
In the literature, there are different approaches to the design of locomotion control systems such as: trajectory based methods, heuristic based methods and biologically inspired methods.
Trajectory based methods
In trajectory based methods, to move a leg in a desired trajectory, the joint angles between limbs are calculated in advance, by using a mathematical model that incorporates both robot and environment parameters, to produce a sequence of actions specifically scheduled. But these methods are not providing any methodology to design a controller. It is only a method to prove the stability of the motion. Therefore, the trajectories have to be designed by trial-and-error or from animal locomotion recording data (Jalal et al., 2009). The most popular stabilization criteria are the Center of Mass (CoM), Center of Pressure (CoP) and Zero Moment Point (ZMP). The gait is stable when one of these criteria remains inside the support polygon (the convex hull formed by the contact points of the feet with the ground).
These methods can generate either static or dynamic stability. The first one prevents the robot from falling down by keeping the CoM inside the support polygon by adjusting the body posture very slowly. Thus minimizing the dynamic effects and allowing the robot to pause at any moment of the gait without falling down. Using this criterion will generally lead to more power consumption since the robot has to adjust its posture so that the CoM is always inside the support polygon. The second one relies on keeping the ZMP or CoP inside the support polygon and this is a necessary and sufficient condition to achieve stability. Dynamic balance is particularly relevant during the single support phase, which means that the robot is standing in only one foot. This generally leads to more fast and reliable walking gaits (Picado et al., 2008).
Heuristic based methods
The major problem with the ZMP or CoP methods are the complexity of the equations used to compute the robot dynamic. With such a level of complexity directly exposed to the robot programmer, it becomes very difficult to have a global view over the robot behavior. This is because heuristics methods were developed to hide the complexity of the problem and make it more accessible.
Heuristic methods have strong similarities with the trajectory based approach. Joint trajectories are also pre-computed from an external optimization process, only the generation strategy differs. This time, heuristic or evolutionary based techniques are used (e.g. genetic
algorithms) to design the desired trajectories (Lathion, 2006).
The most successful approach of this methods is called Virtual Model Control (VMC) (Picado et al., 2008). It is a motion control framework that uses simulations of virtual components to generate desired joint torques. These joint torques create the same effect that
the virtual components would have created, thereby creating the illusion that the simulated components are connected to the real robot. Such components can include simple springs, dampers, dash pots, masses, latches, bearings, non-linear potential and dissipative fields, or any other imaginable component. The generated joint torques create the same effect that the virtual components would create if they were in fact connected to the real robot (Pratt et al., 2001). This heuristic makes the design of the controller much easier. First, it is necessary to
place some virtual components to maintain an upright posture and ensure stability. Virtual
model control has been used to control dynamic walking bipedal robots (Pratt et al., 2001) and an agile 3D hexapod in simulation (Torres, 1996).
Biologically inspired methods
This approach uses CPGs which are supposed to take an important role in animal locomotion. By coupling the neural oscillators signals when they are stimulated through some input, they are able to synchronize their frequencies. In the field of artificial intelligence and robotics, it is possible to build structures that are similar to the neural oscillators found in animals by the definition of a mathematical model (Picado et al., 2008). The term central indicates that sensory feedback (from the peripheral nervous system) is not needed for generating the rhythms. In other words, the CPG has the ability to produce a periodic output from a non-periodic input signal. CPG is a proven fact which exists in animals and its task is to generate the rhythmic movements almost independent of central nervous system. There are a lot of CPG methods and different robotic application have been proposed by different authors (Lee et al., 2007; Loeb, 2001; Nakada, 2003). However, most of the time these CPGs are designed for a specific application and there are very few methodologies to modulate the shape of the rhythmic signals, in particular for on-line trajectory generation and the CPG internal parameters are usually tuned by trial and error methods.
Approaches analysis
Many different solutions have been experimented to achieve stable robot locomotion, from trajectory based methods to biologically inspired approaches. Each method presents different advantages as well as disadvantages. Next, a features summary of each approach under different requirements such as: robot knowledge, perturbation problems, design methodology, physical implementation and control scheme is presented.
• Robot knowledge: the major drawback of the trajectory based and heuristic based methods is that they both required an exact knowledge of the robot model. The CPG approach does not require an exact knowledge of the robot model.
• Perturbation problems: the CPG will recover smoothly and quickly after a perturbation, the ZMP needs external on-line control to deal with perturbations and the VMC is robust against small perturbation.
• Design methodology: the ZMP and VMC have well defined methodology to prove stability and intuitive ways of describing the controller. In the CPG approach, the number of parameters needed to describe the CPG is usually large and the stability is not guaranteed as in trajectory and heuristic based methods.
• Physical implementation: the ZMP is easy to implement in real robots. In the VMC, the control is fast and can be efficiently done on-line. Meanwhile, the CPG is able to generate new trajectories for various speeds, without the necessity to be trained again.
• Control scheme: In the ZMP and VMC, the control is more centralized in a black box connected to the robot. But the CPG will be distributed over the whole robot body, as a virtual spinal cord, this property allows to the robot to continue with the gait generation if some part of the control is missing.
The review shown that the CPG approach presents advantages, over the ZMP and VMC approaches, in the requirements of robot knowledge, perturbation problems, physical implementation and control scheme. For that reasons, more locomotion controllers for legged robots based on CPG are using currently.
Locomotion modeling based on CPG
The activity of the locomotor organs (legs, wings, etc.) generates a propulsive force that leads to locomotion. Each piece of a locomotor organ is rhythmically controlled by a CPG generating the rhythm. These neural networks, controlling each individual organ, interact with others so as to coordinate, in a distributed manner, the locomotor action of a complete specie. Moreover, they also adopt their activity to the surrounding environment through sensory feedback and higher level signals from the central nervous system.
CPGs are often modeled as neurons that have mutually coupled excitatory and inhibitory neurons, following regular interconnection structures. CPGs automatically generate complex control signals for the coordination of muscles during rhythmic movements, such as walking, running, swimming and flying (Delcomyn, 1980; Hooper, 2000; Kimura, Shimoyama & Miura, 2003).
The locomotion patterns can usually be modulated by some parameters, which offers the possibility to smoothly modify the gait (e.g. increase frequency and/or amplitude) or even to induce gait transitions. In CPG design, there are some common assumptions: the nonlinear oscillators are often assumed to be identical, the stepping movements of each limb are controlled by a single oscillator, while interlimb coordination is provided by the connections between the oscillators (Arena et al., 2004). Moreover, the sensory inputs from lower-level central nervous system and signals from higher-level central nervous system can modulate the activity of CPGs. The lower level signals are used for slow movements (low frequency response). Higher level signals are use to produce intelligent behavior and faster movements (higher frequency response). A comprehensive review of utilizing CPGs in robotics can be found in (Ijspeert, 2008), and an interesting overview of the different oscillators utilized for robotics purposes is given in (Buchli et al., 2006).
The vertebrate locomotor system is organized hierarchically where the CPGs are responsible for producing the basic rhythmic patterns, and that higher-level centers (the motor cortex, cerebellum, and basal ganglia) are responsible for modulating these patterns according to environmental conditions. Such a distributed organization presents several interesting features: (i) It reduces time delays in the motor control loop (rhythms are coordinated with mechanical movements using short feedback loops through the spinal cord). (ii) It dramatically reduces the dimensionality of the descending control signals. Indeed the control signals in general do not need to specify muscle activity but only modulate CPG activity. (iii) It therefore significantly reduces the necessary bandwidth between the higher-level centers and the spinal cord (Ijspeert, 2008; Loeb, 2001).
CPG have been modeled with several levels of abstraction as for example: biophysical models, connectionist models, abstract systems of coupled oscillators. In some cases, the CPG models have been coupled to biomechanical simulation of a body, in such case they
are called neuromechanical models. Detailed biophysical models are constructed based on the Hodgkin-Huxley type of neuron models. That is, neuron models that compute how ion pumps and ion channels influence membrane potentials and the generation of action
potentials. In particular, the cells excite themselves via fast feedback signals while they inhibit themselves and other populations via slower feedback signals. In some cases, the pacemaker properties of single neurons are investigated. While most models concentrate
on the detailed dynamics of small circuits, some models address the dynamics of larger populations of neurons, for instance the generation of traveling waves in the complete lamprey swimming CPG (Arena, 2001). Connectionist models use simplified neuron models
such as leaky-integrator neurons or integrate-and-fire neurons. This connectionist model has
shown that connectivity alone is sufficient to produce an oscillatory output. The goal of these models is on how rhythmic activity is generated by network properties and how different oscillatory neural circuits get synchronized via interneuron connections (Ijspeert, 2008).
Other extensively used oscillators include phase oscillators (Buchli & Ijspeert, 2004; Matsuoka, 1987). Most of the oscillators have a fixed waveform for a given frequency. In some cases, closed-form solutions or specific regimes, as for example phase-locked regimes, can be analytically derived but most systems are solved using numerical integration. Several neuromechanical models have been developed. The addition of a biomechanical model of the body and its interaction with the environment offers the possibility to study the effect of sensory feedback on the CPG activity.
Finally, oscillator models are based on mathematical models of coupled nonlinear oscillators to study population dynamics. In this case, an oscillator represents the activity of a complete oscillatory center (instead of a single neuron or a small circuit). The purpose of these models is not to explain rhythmogenesis (oscillatory mechanisms are assumed to exist) but to study how inter-oscillator couplings and differences of intrinsic frequencies affect the synchronization and the phase lags within a population of oscillatory centers. The motivation for this type of modeling comes from the fact that the dynamics of populations of oscillatory centers depend mainly on the type and topology of couplings rather than on the local mechanisms of rhythm generation, something that is well established in dynamical systems theory (Ijspeert & Crespi, 2007).
CPG-based locomotion design for quadruped robots
The locomotion control research field has been pretty active and has produced different approaches for legged robots. But the ability for robots to walk in an unknown environment is still much reduced at the time. Experiments and research work have addressed the feasibility of the design of locomotion control systems of legged robots taking inspiration from locomotion mechanisms in humans and animals. Legged locomotion is performed in rhythmic synchronized manner where a large number of degrees of freedom is involved so as to produce well-coordinated movements.
As described previously, one of the main drawbacks of CPGs is that there are few learning methodologies to generate the rhythmic signals and their parameters are usually tuned by trial and error methods. Learning and optimization algorithms can be used in different ways.
The approaches can be divided into two categories: supervised learning and unsupervised learning. Supervised learning techniques can be applied when the desired rhythmic pattern that the CPG should produce is known. The desired pattern can then be used to define an explicit error function to be minimized. Such techniques can sometimes be used for designing CPGs, but they are restricted to situations where suitable patterns are available (e.g. they are obtained from kinematic measurements of animals). Some examples of these techniques
are learning for vectors fields (Okada et al., 2002), gradient descent learning algorithms (Pribe et al., n.d.) and statistical learning algorithms (Nakanishi et al., 2004). Unsupervised learning techniques are used when the desired behavior of the CPG is not defined by a specific
desired pattern (as in supervised learning), but by a high-level performance criterion, for instance, moving as fast as possible. Among unsupervised learning techniques, stochastic population-based optimization algorithms such as evolutionary algorithms have extensively
been used to design CPG-like models (Ijspeert, 2008). The parameters that are optimized are usually the synaptic weights in fixed neural network architectures and coupling weights in systems of coupled oscillators.
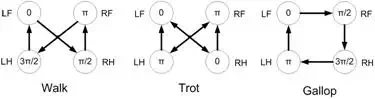
Fig. 1. Configurations of typical gait patterns in quadruped locomotion and their relative phases among the limbs.
Van Der Pol oscillator model
There are several models for neural oscillators to model the basic CPG to control a limb, such as the Amari-Hopfield model (Amari, 1988), Matsuoka model (Billard & Ijspeert, 2000) and Van Der Pol model (Van Der Pol B, 1928). For this work, the basic cell is modeled by a Van Der Pol (VDP) oscillator which is a relaxation oscillator governed by a second-order differential equation (equation 1):
x¨ − α( p2 − x2 )x˙ + ω2 x = 0 (1)
where x is the output signal from the oscillator, α, p and ω are the parameters that tune the properties of oscillators. In general, α affects the shape of the waveform, the amplitude of x depends largely on the parameter p. When the amplitude parameter p is fixed, the output frequency is highly dependent on the parameter ω. However, a variation of parameter p can slightly change the frequency of the signal, and α also can influence the output frequency.
Quadruped gaits
A simplified mathematical model of CPG-based locomotion consists of using one cell per limb and replacing each cell by a nonlinear oscillator. Thus, quadruped gaits are modeled by coupling four nonlinear oscillators, and by changing the connections among them, it is possible to reproduce rhythmic locomotion patterns. In rhythmic movements of animals, transition between these movements is often observed. As a typical example, horses choose different locomotive patterns in accordance with their needs, locomotive speeds or the rate of energy consumption. In addition, each gait pattern is characterized by relative phase among the limbs (Dagg, 1973). Figure 1 shows the typical horse gait pattern configurations and theirs relatives phases between the limbs. Here, LF, LH, RF, and RH stand for left forelimb, left hindlimb, right forelimb, and right hindlimb. In the rest of this work, LF, RF, RH and LH will be refer as X1, X2, X3 and X4 , respectively.
The mutual interaction among the VDP oscillators in the network produces a gait. By changing the coupling weights, it is possible to generate different gaits. The dynamics of the ith coupled oscillator in the network is given by
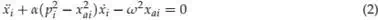
For i = 1, 2, 3, 4 , where xi is the output signal from oscillator i, xai denotes the coupling contribution of its neighbors given by the equation 3:
xai = ∑ wij xj (3)
j
where wij is the coupling weight that represents the strength of ith oscillator over the jth oscillator. The generation of the respective gaits depends on the values of the oscillators parameters and the connection wights among oscillators.
The analysis of the behavior reported in (Barron-Zambrano & Torres-Huitzil, 2011) shows that the sign of the coupling weight determines the phase difference. For inhibitory connections, the phase lag is around of 360/n to particular values of wij , where n is the number of coupled oscillators. For excitatory connections, the phase difference is equal to zero. Finally, the matrix built for the connection weights, wij , might be symmetrical and regular.
GA-based approach for gait learning
To efficiently search for CPG parameters a genetic algorithm for oscillator parameters estimation was used. A genetic algorithm is a powerful optimization approach that can work in large-dimensional, nonlinear, and, often, largely unknown parameter spaces. In the simplest form of gait evolution, functional forward locomotion is the only goal and no sensor inputs are used. Gait learning is a form of locomotion learning, but it might be considered a somewhat more difficult problem in legged robots. The search space is represented by the genome defining the controller representation (or controller and morphology representation). Each evolvable parameter of the genome defines a dimension of the search space, and the fitness landscape is then given by the manifold defined by the fitness of each point in the search space.
The tuned method is divided into two stages and the robot controller was represented by a string of real numbers that describe oscillators and their connectivity. The first one estimates the oscillator parameters and the second one calculates the values of wij to produce the locomotion pattern. The two stages work in sequential way.
The first stage estimates the parameters [α, p, ω] to generate a specific wave in frequency and amplitude. Here, the oscillators parameters correspond to the gene and represent the organization of an individual n in a group of population N. The individual, n, is represented by the concatenation of parameters in order shown in equation 4, where each parameter was represented by real numbers of 32-bit:
n = [α pω] (4) Each individual n is evaluated according to the next fitness function which is minimized by
the GA:
f itness p = abs(( Ad − A p ) ∗ ( fd − DFT(So ))) (5)
where Ad is the desired amplitude of the signal, fd is the desired frequency, A p is the amplitude of the generated pattern, So is the pattern generated by the oscillator with the individual n and DFT is the Discrete Fourier Transform. Simulation of So is generated by around of 50 seconds by each individual, n, and only the last 5 seconds are considered for the DFT computation. This is to ensure a stable signal, in frequency and amplitude, and to reduce the amount of data to be processed. Figure 2 shows a block diagram of this stage.
The GA ranks the individuals according the fitness function. As result of ranking, the best individuals remain in the next generation without modification. For this stage, 2 individuals remain without modification and go to the next generation. By using the crossover operation, other individuals in the next generation are created by combining two
Fig. 2. Block diagram of first stage. It estimates the oscillator parameter values, [α, p, ω], to produce a signal with specific frequency and amplitude.
individuals. Furthermore, the remaining individuals are randomly modified by mutation. The probabilities of crossover and mutation are set to be 0.8 and 0.2, respectively.
The second stage performs the synchronization among the oscillator outputs. The generation of different gaits needs patterns with specific phase amount the output signals, see figure 1. The stage computes the value of wij . To produce a desired phase is not enough only with connection weights, it is necessary to calculate the initial conditions of each oscillator, x1..4 , too. For that purpose, in the second stage each individual, n, has five values in order to generate a specific phase in the network. The values in the gene are organized from the right to left. The first four values are the initial values for each oscillator, x1..4 . And the fifth value codes the connection weight, w. The equation 6 shows the presentation of n in this stage.
n = [wx4 x3 x2 x1 ] (6)
where the initial values and connection weight were represented by real numbers.
The GA only needs estimate one value of w for one gait and by changing the algebraic sign it is possible to generate the rest of the gaits. The fitness function is based on the phase among the patterns. To estimate the phase among the signals, the correlation was used. The oscillator
labeled as LF (X1) is the reference signal, phase equal to zero, and the other signals are shifted with respect to this signal. The fitness function to evaluate the individual is given by equation
7. Here, the GA minimizes the value of the fitness function.
f itnessω = abs(90 − phase(x1 , x3 )) + abs(90 − phase(x3 , x2 )) + abs(90 − phase(x2 , x4 )) (7)
where phase( xi , xj ) is the phase between the ith and jth oscillator. The simulation of x1..4 is generated by around of 50 seconds by each n and only the last 10 seconds are considered for the phase estimation. Figure 2 shows a block diagram of the second stage.
Related work of hardware implementations
Nowadays, many works have aimed to develop robust legged locomotion controllers (Fujii et al., 2002; Fukuoka et al., 2003; Susanne & Tilden, 1998). The design CPG-based control systems has been difficult given that the simulation of even rather simple neural network models requires a computational power that exceeds the capacity of general processors. For that reason, CPG dedicated hardware implementations, both analog and digital, have received more attention (Nakada, 2003). On one hand, CPGs have been implemented using
Fig. 3. Block diagram of second stage. It finds the values of coupling, wij and the initial values of x1..4 .
microprocessors providing high accuracy and flexibility but those systems consume high power and occupy a large area restricting their utility in embedded applications. On the other hand, analog circuits have been already proposed, being computation and power efficient but they usually lack flexibility and dynamics and they involve large design cycles.
Relatively few works have focused on adopting the hardware technology to fully practical embedded implementations. Examples of this adaptation using analog circuit are presented by (Kier et al., 2006; Lee et al., 2007; Lewis et al., 2001; Nakada, 2003). In the first one, Nakada et al present a neuromorphic analog CMOS controller for interlimb coordination in quadruped locomotion. Authors propose a CPG controller with analog CMOS circuits. It is capable of producing various rhythmic patterns and changing these patterns promptly. Lewis at al constructed an adaptive CPG in an analog VLSI (Very Large Scale Integration) chip, and have used the chip to control a running robot leg.
They show that adaptation based on sensory feedback permits a stable gait even in an under actuated condition: the leg can be driven using a hip actuator alone while the knee is purely passive. Their chip has short-term on board memory devices that allow the continuous, real-time adaptation of both center-of-stride and stride amplitude. In addition, they make use of integrate-and-fire neurons for the output motor neurons. Finally, the authors report that their abstraction is at a higher level than other reported work, which lends itself to easier implementation of on-chip learning. Kier et al present a new implementation of an artificial CPG that can be switched between multiple output patterns via brief transient inputs. The CPG is based on continuous-time recurrent neural networks (CTRNNs) that contain multiple embedded limit cycles. The authors designed and tested a four-neuron CPG chip in AMI’s 1.5 µm CMOS process, where each neuron on the chip implements the CTRNN model and is fully programmable. The authors report the measured results from the chip agree well with simulation results, making it possible to develop multi-pattern CPGs using off-line simulations without being concerned with implementation details. Lee at al report a feasibility study of a central pattern generator-based analog controller for an autonomous robot. The operation of a neuronal circuit formed of electronic neurons based on Hindmarsh-Rose neuron dynamics and first order chemical synapses modeled. The controller is based on a standard CMOS process with 2V supply voltage. Simulated results show that the CPG circuit with coordinate controller and command neuron is viable to build adaptive analog controller for autonomous biomimetic underwater robots. Finally, a biologically inspired swimming machine is presented by Arena in (Arena, 2001).
The system used to generate locomotion is
an analog array of nonlinear systems known as Cellular Neural Networks (CNN). The CNN is defined as a two-dimensional array of M × N identical cells arranged in a rectangular grid, where each cell was defined as the nonlinear first order circuit. The author reports that the application to service robot further underlines that CNNs can be used as powerful devices to implement biologically inspired locomotion and swimming.
Another solution to implement the CPG is using FPGAs as the hardware platform. The CPG is programmed in either VHDL or Verilog and download it onto the FPGA. This approach provide the hardware efficiency with software flexibility. In (Torres-Huitzil, 2008), Torres and Girau present an implementation of a CPG module based on the Amari-Hopfield structure into pure FPGA hardware. In their work, they have chosen to attached the CPG implementation to a Microblaze soft-core processor running uclinux. By doing this, they achieve the computation speed from having the CPG running the mathematical operations in the FPGA hardware making it possible to achieve some degree of parallelization in the calculations and then having the soft-core CPU free to handle other high level control algorithms and this could change the control parameters on the CPG implementation. Barron et al in (Barron-Zambrano et al., 2010b) present a FPGA implementation of a controller, based on CPG, to generate adaptive gait patterns for quadruped robots. The proposed implementation is based on an specific digital module for CPGs attached to a soft-core processor so as to provide an integrated and flexible embedded system. Experimental results
show that the proposed implementation is able to generate suitable gait patterns, such as walking, trotting, and galloping.
Other CPGs implementations are using microprocessor. It gives the designer more freedom, because it is not constrained by the difficulty of designing e.g. a differential analog circuits.
These implementations using a scheme where the control is distributed trough the robotbody. The first implementation example of these is presented by (Inagaki et al., 2006). In that work, Inagaki et al proposed a method to control gait generation and walking
speed control for an autonomous decentralized multi-legged robot using CPGs. The robot locomotion control is composed by subsystems. Each subsystem controls a leg and has a microcomputer. The subsystems are connected mechanically and communicate with
neighbors. Each microcomputer calculates the dynamics of two oscillators, sends and receives the dynamic results from neighbor subsystems. The gait generation and the walking speed control are achieved by controlling the virtual energy of the oscillators (Hamiltonian). A real
robot experiment showed the relationship to the Hamiltonian, the actual energy consumption and the walking speed. The effectiveness of the proposed method was verified. The proposed controller can be generalized as a wave pattern controller, especially for robots
that have homogeneous components. In (Crespi & Ijspeert, 2006), Crespi and Ijspeert proposed an amphibious snake robot designed for both serpentine locomotion (crawling) and swimming. It is controlled by an on-board CPG inspired by those found in vertebrates.
The AmphiBot II robot is designed to be modular: it is constructed out of several identical segments, named elements. Each element contains three printed circuits (a power board, a proportional-derivative motor controller and a small water detector) connected with a flat
cable, a DC motor with an integrated incremental encoder, a set of gears. The elements are connected (both mechanically and electrically) using a compliant connection piece fixed to the output axis. The main contribution of this article is a detailed characterization of how the CPG
parameters (i.e., amplitude, frequency and wavelength) influence the locomotion speed of the robot.
The related works present control schemes for robot locomotion based on biological systems under different implementation platforms. The schemes compute the walk pattern in a parallel way through the specialized either systems or coupled subsystems. The CPG control can be implemented by different approaches (analog circuits, reconfigurable hardware and digital processors). The analog circuit implementations present a good performance between power and energy consumption, but they have a large design cycle. For that, these approaches are useful in robots with either limited storage of energy or data processing with real time constraints. In the second approach is possible to implement CPG control with real time constraint sacrificing the energy performance. These implementations have smaller design cycle than the analog circuit implementations. The approach is ideal to be used in the early robot design stages. The last approach presents a high flexibility because it is not constrained by the difficulty of designing. The design cycle is shorter but it has the worst energy performance. Furthermore, those systems occupy a large area restricting their utility in embedded applications.
The analyzed implementations shown several common features. The first one is that they are reconfigurable. The second one, they are capable to adapt oneself to different environments.
The most of the implementations presents a scheme where the control is distributed trough the robot body or they are implemented through the interaction of basic elements. These similar features are seen in animal locomotion tasks.
CPG hardware implementation for a quadruped robot
In this section, we describe the architecture of the CPG controller for interlimb coordination in quadruped locomotion. First, the design considerations for the implementation are presented. Next, the basic Van Der Pol Oscillator that constitute a part of the CPG network is given. Finally, the architecture of the complete system is described.
Design considerations
The Van Der Pol oscillator is suitable for CPG implementation as a digital circuit but two main factors for an efficient and flexible FPGA-based implementation should be taken into account: a) arithmetic representation, CPG computations when implemented in general microprocessor-based systems use floating point arithmetic. An approach for embedded implementations is the use of 2s complement fixed point representation with a dedicated wordlength that better matches the FPGA computational resources and that saves further silicon area at the cost of precision, and b) efficiency and flexibility, embedded hard processor cores or configurable soft processors developed by FPGA vendors add the software programmability of optimized processors to the fine grain parallelism of custom logic on a single chip (Torres-Huitzil, 2008). In the field of neural processing, several applications mix real-time or low-power constraints with a need for flexibility, so that FPGAs appear as a well-fitted implementation solution.
Most of the previous hardware implementation of CPGs are capable of generating sustained oscillations similar to the biological CPGs, however, quite a few have addressed the problem of embedding several gaits and performing transitions between them. One important design consideration in this work, is that the FPGA-based implementation should be a platform well suited to explore reconfigurable behavior and dynamics, i.e., the platform can be switched between multiple output patterns through the application of external inputs.
(a) (b)
Fig. 4. (a) Digital hardware architecture for the Van Der Pol oscillator and (b) average error as a function of the bit precision used in the basic blocks.
Module of Van Der Pol oscillator
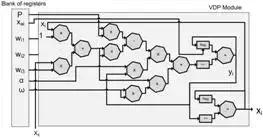
From the analysis of Van Der Pol equation, Eq. 2, three basic operations were identified: addition, subtraction and multiplication. Thus, one block for each operation was implemented with 2’s complement fixed-point arithmetic representation. Figure 4(a) shows a block diagram for the hardware implementation of the discretized VDP equation. In the first stage, the value of xai (equation 3) is calculated: this value depends on the xi -neighbors and the coupling weight values. This stage uses four multipliers and one adder. The square values of p, xai and ω are calculated in the second stage, it uses three multipliers. In the third stage, the values of α ∗ yi and p2 − xai are calculated, one multiplier and a subtracter are used. The fourth stage computes the values of α ∗ yi ∗ ( p2 − xai ) and w2 ∗ xai . This stage uses two multipliers.
For the integration stage, the numerical method of Euler was implemented by using two shift registers and two adders. The integration factor is implemented by a shift register, which shifts six positions the values of y˙i and x˙i to provide an integration factor of 1/64. The block labeled as Reg stands for accumulators that hold the internal state of the VPD oscillators. Finally, the values yi and xi are obtained.
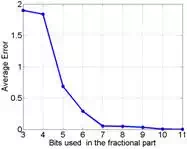
The size word for each block was 18-bit fixed point representation with 11-bit for the integer part and 7-bit for the fractional part. Figure 4(b) shows the amplitude average error using different precisions for the fractional part. The errors were obtained from the hardware
implementation. Plot shows that the average error decreases as the resolution of the input variables is incremented. This reduction is not linear, and the graphic shows a point where such reduction is not significant. Seven bits were chosen as a good compromise between the
fractional part representation and its average error.
Quadruped gait network architecture
In the CPG model for quadruped locomotion all basic VDP oscillators are interconnected through the connection weights (wi j). In order to overcome the partial lack of flexibility of the CPG digital architecture, it has been attached as a specialized coprocessor to a microblaze processor following an embedded system design approach so as to provide a high level interface layer for application development. A bank of registers is used to provide communication channels to an embedded processor. The bank has twenty-three registers and it receives the input parameters from microblaze, α, p2 , ω2 , wij and the initial values of each oscillator. The architecture sends output data to specific FPGA pins. Figure 5 shows
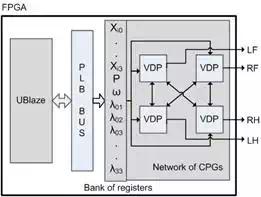
Fig. 5. Complete architecture for embedded implementation of a CPG-based quadruped locomotion controller.
a simplified block diagram of the VPD network interfacing scheme to the bank registers and microblaze processor.
Experimental results
GA–based method results
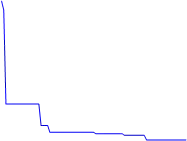
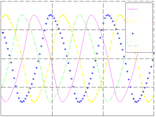
The proposed GA-based method was implemented in Matlab and its results were tested through hardware implementation reported in (Barron-Zambrano et al., 2010b). For the implementation of the GA, the specialized toolbox of Matlab was used. The parameters used to estimate the variables of the oscillator were: a population of 30 individuals and 200 generations. The probabilities of crossover and mutation are set to be 0.8 and 0.2 respectively. The method has an average error with the desired frequency of ±0.03 Hz and with the desired amplitude of ±0.15. Simulations show the state of the parameters in different generations, the first plot shows the simulations in the 2nd population generation. The generated signal in the early generations is periodic but it has low value of frequency and amplitude respect to the actual desired value. The second plot shows a signal with periodic behavior, 7th generation, but with a different frequency with respect to the desired frequency. Finally, the last plot shows the pattern with the desired frequency, 1 Hz, and amplitude, 2.5. The final parameters [α, p, ω] estimated for the method are [0.705, 0.956, 4.531].
Figure 6 shows the behavior of the fitness values at each generation for the oscillator
parameters, plot 6(a), and for the network weights and initial conditions of x1..4 , plot 6(b). In both cases, the fitness function values decrease suddenly in the early stages of tuning. Also, plots show that the method needs a reduced number of generations to tune the oscillator and the network.
In a second step, the estimation of wih and the initial values of x1..4 is computed. The parameters used for this step were: a population of 40 individuals and 300 generations. The probabilities of crossover and mutation are set to be 0.5 and 0.2 respectively. In the test, the desired pattern is a walk gait. This pattern has a phase of 90 degrees among the signal in fixed order, X1 − X3 − X2 − X4. Only, the walk matrix was estimated by the method. It is possible to generate the trot and gallop gait with the walk matrix and only changing the initial condition of x1..4 , but it is impossible to switch from one gait to another when the gait
0.5
0.4
0.3
![]() 0.2
0.2
0.1
 0
0
0 5 10 15 20 25
Generations
(a)
150
![]() 100
100
50
0
20 40 60 80
Generations
(b)
Fig. 6. (a) Fitness convergence plots for the first stage, oscillator parameters and (b) for the second stage, network weights and initial conditions of x1..4 .
Gait Walk Trot Gallop
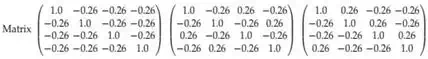
| |
Table 1. Weight matrix to configure the CPG network
is stable. Then, the remaining matrices, trot and gallop, were calculated using the behavior analysis presented in (Barron-Zambrano & Torres-Huitzil, 2011). The analysis shows that the combination of inhibitory and excitatory connections is able to modify the phase among the oscillators. Thus, it is possible to generate different gaits from walk matrix. To change the connections from inhibitory to excitatory type, and vice-versa, is only necessary to change the algebraic sign of the values in the gait matrix.
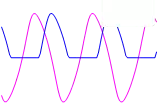
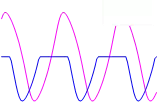
In the trot gait, the front limbs have the reverse phase and the limbs on a diagonal line move synchronously. From that, to generate the trot gait is necessary to change the algebraic sign in the matrix of weights for limbs on a diagonal line. The gallop has similarities with the walk gait, the phase is equal to 90 degrees but the order is different, X1 − X2 − X3 − X4. Therefore, the design of a new matrix for this gait is necessary. The gallop matrix is obtained only by changing the algebraic sign in the one connections off-diagonal, this produces a phase equal to 90 degrees among the limbs. Table 1 shows the matrix weights for the three basic gaits, walk, trot and gallop with parameters α, p and ω equal to [1.12, 1.05, 4.59] and initial conditions x1..4 = [2.44, 4.28, −1.84, 2.71].
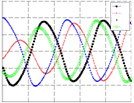
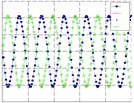
Figure 7 shows the evolution of network weights and the initials condition of x. The plot 7(a) shows the pattern generated when the second stage starts. It shows a synchronized pattern where all signals have the same phase. The evolution of population shows how the signals
start to have different phases, figure 7(b). Figure 7(c) shows that the method found the correct weight and the initial values of x1..4 to generate the walk gait pattern. Finally, figure 7(d) and 7(e) show the pattern generated by the trot and gallop gaits with matrices estimated from the
walk gait matrix.
| 3 | 3 | 3 | ||||||||||||||||||||||||||||||||||||
| X1X2 | X1X2 | X1X2 | ||||||||||||||||||||||||||||||||||||
| 2 | X3 | 2 | X3 | 2 | X3 | |||||||||||||||||||||||||||||||||
| X4 | X4 | X4 | ||||||||||||||||||||||||||||||||||||
| 1 | 1 | 1 |
 0
0
![]() −1
−1
−2
−3
5 6 7 8 9 10
Time (s)
(a)
 0
0
![]() −1
−1
−2
−3
5 6 7 8 9 10
Time (s)
(b)
 0
0
![]() −1
−1
−2
−3
5 6 7 8 9 10
Time (s)
(c)
 3 3
3 3
X1
X2
2 X3 2
X4
![]()
![]() 1 1
1 1
X1
X2
X3
 X4
X4
0 0
−1 −1
−2 −2
−3
5 6 7 8 9 10
Time (s)
(d)
−3
5 6 7 8 9 10
Time (s)
(e)
Fig. 7. (a)-(c)Evolution of pattern, in different generations, generated by the walk gait. (d)-(e) Pattern generated by the trot and gallop gait with matrices estimated from the walk gait matrix.
Physical implementation
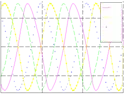
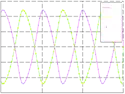
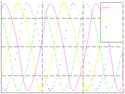
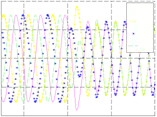
The CPG digital architecture has been modeled using the Very High Speed Integrated Circuits Hardware Description Language (VHDL), and synthesized using the ISE Foundation and EDK tools from Xilinx targeted to the Virtex-4 FPGA device. In the hardware implementation test, a C-based application was developed on the microblaze embedded processor to set the values of the parameters in the CPG module. The implementation was validated in two ways. The first one, the results were sent to the host computer through serial connection to visualize the waveforms generated by the module. Then, the hardware waveforms were compared with the software waveforms. In the second way, results were sent to digital-analog converter (DAC) and the output signal from DAC was visualized on a oscilloscope. Figure 8 shows, the periodic rhythmic patterns corresponding to the gaits (walk, trot, gallop) generated by hardware implementation. The values of the weight matrix to configure the CPG network are shown in table 1. The initial value, x1..4, the parameter values, [α, p, ω], and the weight value, wij , were calculated automatically with a GA implementation.
The last CPG-hardware test was done through Webots robot simulator software. In this simulation the network with 8 VPD modules was used. Figure 9 shows, the walking locomotion pattern, in the bioloid robot simulator, and the periodic oscillations for the
different joints, limbs and knees, produced by the hardware implementation. Figures 9(a)- 9(h) show the specific bioloid joint positions corresponding to the time labels shown in the walk time graph. Figures 9(i)- 9(k) show the phase relationship between the knee and
limb joints in the right forelimb and hindlimb during walking. Finally, in figure 9(l) a time graph to show transition between walking and trotting is presented. Locomotions patterns for trot and gallop, and the transitions between them, were also tested.
3
X1
2 X2 2
![]() X3 1
X3 1
X4
 0 0
0 0
−1
−2 −2
−3
X1
X2 2
X3
 X4
X4
0
![]() −2
−2
X1
X2
X3
 X4
X4
7 8 9 10
Time (s)
![]() (a) Walk
(a) Walk
7 8 9 10
Time (s)
(b) Trot
7 8 9 10
Time (s)
(c) Gallop
Fig. 8. (a)-(c) Three basic gaits for quadruped locomotion
Future work
In general, the discussion of future work will be focused in three goals: (a) to scale up the present approach to legged robots with several degrees of freedom to generate complex rhythmic movements and behavior, (b) integrate visual perception information to adapt the locomotion control in unknown environment, (c) incorporate the feedback from the robot body to improve the generation of patterns.
Network scalability
Nowadays, in robotics, the decentralization of control is an approach increasingly used in the design stage. In this approach, the robot control consists of group of modules where each module process the information in a local way. Then, the information of each module is sent to neighbor modules to produce a global result. One of the remarkable features of modular robots control is its scalability. This ability is important to achieve the best configuration required for doing the task, it is also useful in self-repair by separating faulty modules and replacing them with other modules (Murata & Kurokawa, 2007). Self-organization and distributed intelligence characterized by distribution of processing, decentralization of control and sensing tasks and modularization of components, have become essential control paradigms (Mutambara & Durrant-Whyte, 1994).
In the hardware architecture context, the scalability can be defined as the ability to increase the architecture throughput without a complete re-design, using additional hardware, in order to meet a user need. In other words, the architecture must be able to adapt oneself to robots with more degrees of freedom only adding the necessary modules. The first example of hardware scalability is presented in (Barron-Zambrano et al., 2010a). In this work, the scalability of a CPG, which control a quadruped robot with 1 DOF per limb, was the necessity to control a quadruped robot with two degrees of freedom per limb. In this case, the locomotion control system will be scalable a network with eight VDP oscillators as suggested in most works reported in the literature (Fujii et al., 2002; Kimura, Fukuoka, Hada & Takase, 2003).
Visual perception information
Locomotion and perception have been treated as separate problems in the field of robotics. Under this paradigm, one first solves the vision problem of recovering the three-dimensional geometry of the scene. This information is then passed to a planning system that has access to an explicit model of the robot (Lewis & Simo, 1999). This solution is computationally intense and too slow for real-time control using moderate power CPUs. Furthermore, this approach

 (a) (b) (c) (d)
(a) (b) (c) (d)
(e) (f) (g) (h)
4
![]() 2
2
0 (a)
(b)
(c)
 (e)
(e)
(f)
(g)
4
X1
X2
![]() X3 2
X3 2
X4
0
−2
(d)
−2
(h)
−4
7 8 9 10
Time (s)
(i) Walk time graph
| X2X2 knee |
−4
7 8 9 10
Time (s)
(j) Right forelimb
| X3X3 knee |
4 4
|−−−−−Walk−−−−−−−| X1
X2
![]()
![]() 2 2 X3
2 2 X3
 X4
X4
0 0
−2 −2
−4
7 8 9 10
Time (s)
(k) Right hindlimb
|−−−−−−−Trot−−−−−−|
−4 8 10 12 14
Time (s)
(l) walk to trot transition
Fig. 9. (a)-(h) Walking locomotion patter snapshots for the bioloid robot simulator. (i) Walk time graph for different joints. (j)-(k) Oscillation patterns for the right forelimbs, hindlimbs and knees. (l) Waveforms during transition between walking and trotting.
does not exploit the fact that the walking machine will be presented with a similar situation again and again.
Recently, approaches consider to eliminate the intermediate explicit model and consider creating a direct coupling of perception to action, with the mapping being adaptive and based on experience. Also, continuous visual input is not necessary for accurate stepping. Not all visual samples have the same potential for control limb movements. Samples taken when the foot to be controlled is in stance are by far more effective in modulating gait. It has been suggested that during stepping visual information is used during the stance phase in a feed forward manner to plan and initiate changes in the swing limb trajectory (Hollands & Marple-Horvat, 1996; Patla et al., 1996).
Taken together, this may indicate that gait is modulated at discrete intervals. This modulation may be a program that depends on a brief sampling of the visual environment to instantiate it (c.f. (Patla Aftab E., 1991) ). This hypothesis is intriguing because it implies that after a brief sample it is not necessary to store an internal representation of the world that needs to be shifted and updated during movement. This shifting and updating is problematic for both neural and traditional robotics models (Lewis & Simo, 1999).
Feedback from the robot body
Studies of mechanisms of adaptive behavior generally focus on neurons and circuits. But adaptive behavior also depends on interactions among the nervous system, body and environment: sensory preprocessing and motor post-processing filter inputs to and outputs from the nervous system; co-evolution and co-development of nervous system and periphery create matching and complementarity between them; body structure creates constraints and opportunities for neural control; and continuous feedback between nervous system, body and environment are essential for normal behavior. This broader view of adaptive behavior has been a major underpinning of ecological psychology and has influenced behavior-based robotics. (Chiel & Beer, 1997).
Recent work in the field of autonomous robotics has emphasized that intelligent behavior is an emergent property of an agent embedded in an environment with which it must continuously interact. The goal is to integrate information of the robot status with the CPG. The robot will
be equipped with different sensors such as bumpers and accelerometers. These sensor signals could be added as coupling terms in the differential equation in the oscillator model. This can be able to simplify the control, allowing them to traverse irregular terrain and making them
robust to failures.
Conclusions
The quadruped locomotion principles were studied and analyzed. It is feasible to generate locomotion patterns by coupling the neural oscillators signals that are similar to the neural oscillators found in animals by the definition of a mathematical model. The GA based approach takes advantage that the fitness function works directly with the oscillator and the network. It makes possible consider other restriction as the power consumption and it does not need knowledge of the robot dynamic to generate the pattern gait. The GA based approach uses small population, some tens individuals, and limited generations, some hundreds generations, ideal to be processed on computers with reduced resources. The applications only estimate the matrix for walk gait. Furthermore, it is possible to build the matrix for gallop and trot gaits using the walk gait matrix. This reduces the number of operations necessary to estimate the matrix for each gait
The hardware implementation exploits the distributed processing able to carry out in FPGA devices. The presented examples show that the measured waveforms from the FPGA-based implementation agree with the numerical simulations. The architecture of the elemental Van Der Pol oscillator was designed and attached as a co-processor to microblaze processor. The implementation provides flexibility to generate different rhythmic patterns, at runtime, suitable for adaptable locomotion and the implementation is scalable to larger networks. The microblaze allows to propose an strategy for both generation and control of the gaits, and it is suitable to explore the design with dynamic reconfiguration in the FPGA. The coordination of joint of a legged robot could be accomplished by a simple CPG-based network extremely small suitable for special-purpose digital implementation. Also, the implementation takes advantage of its scalability and reconfigurability and it can be used in robots with different numbers of limbs.



Comments are closed